Research

All my papers can be found here, and my PhD thesis is here.

Below are some topics and projects that I have worked on.

The Hadamard Gate in Quantum Computation

I undertook this project with my two PhD supervisors, Paul Skrzypczyk and Noah Linden, and our paper was recently published in Quantum.

Paper: The Hadamard gate cannot be replaced by a resource state in universal quantum computation, Quantum, 2024.   Slides   Talk

Abstract

We consider models of quantum computation that involve operations performed on some fixed resourceful quantum state. Examples that fit this paradigm include magic state injection and measurement-based approaches. We introduce a framework that incorporates both of these cases and focus on the role of coherence (or superposition) in this context, as exemplified through the Hadamard gate. We prove that given access to incoherent unitaries (those that are unable to generate superposition from computational basis states, e.g. CNOT, diagonal gates), classical control, computational basis measurements, and any resourceful ancillary state (of arbitrary dimension), it is not possible to implement any coherent unitary (e.g. Hadamard) exactly with non-zero probability. We also consider the approximate case by providing lower bounds for the induced trace distance between the above operations and \(n\) Hadamard gates. To demonstrate the stability of this result, this is then extended to a similar no-go result for the case of using \(k\) Hadamard gates to exactly implement \(n>k \) Hadamard gates.

Property Testing of Entanglement

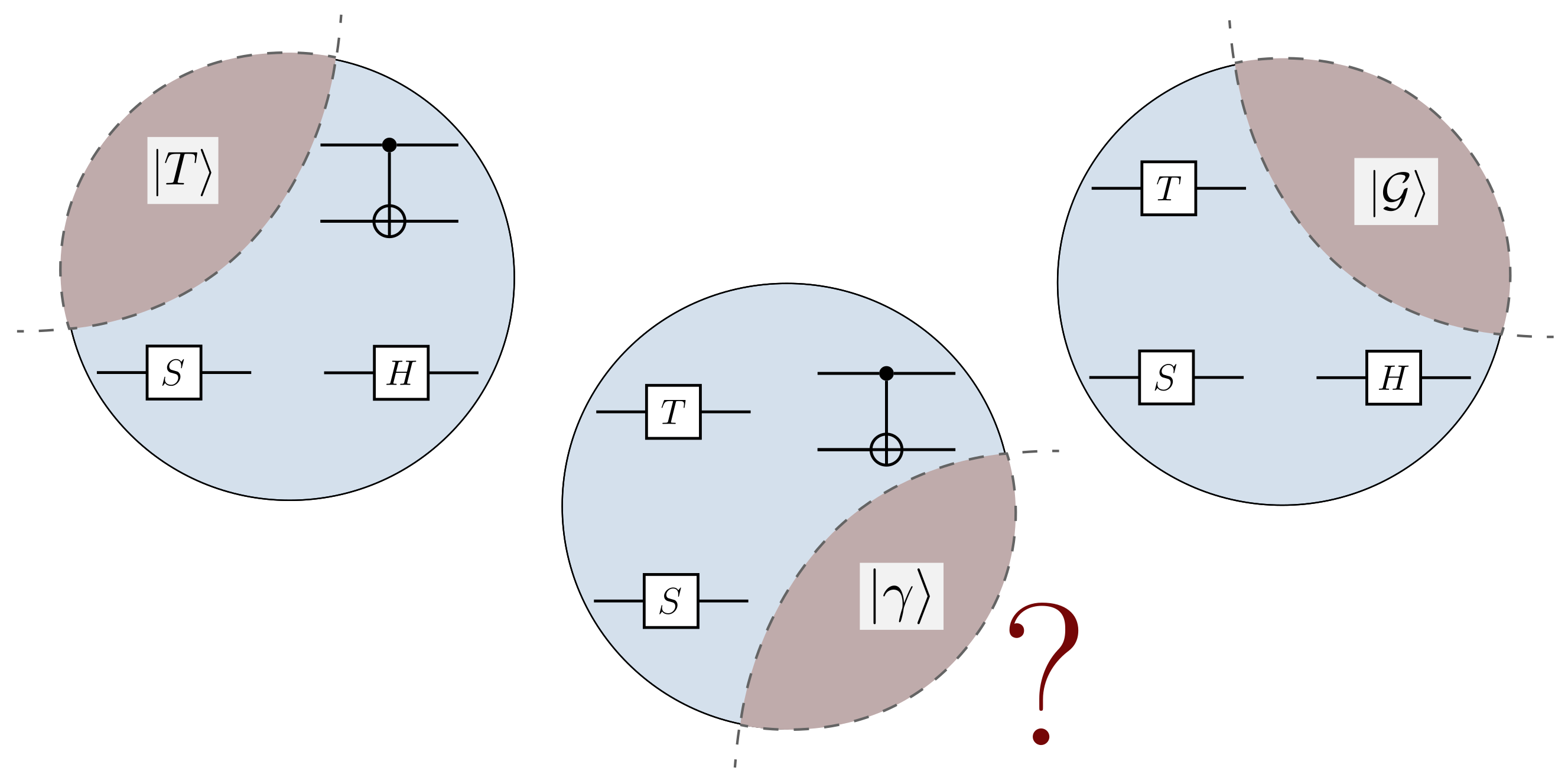
This work relates to the question: how many copies of a multipartite quantum state are needed to determine if the state is product across some bipartition? This work was in collaboration with Ashley Montanaro, and our paper is essentially a long mathematical proof. A preprint is available, and the manuscript is currently under review at journals.

Paper: Testing multipartite productness is easier than testing bipartite productness, arXiv, 2024.

Abstract

We prove a lower bound on the number of copies needed to test the property of a multipartite quantum state being product across some bipartition (i.e. not genuinely multipartite entangled), given the promise that the input state either has this property or is \(\epsilon\)-far in trace distance from any state with this property. We show that \(\Omega(n / \log n) \) copies are required (for fixed \(\epsilon \leq \frac{1}{2}\)), complementing a previous result that \(O(n / \epsilon^2)\) copies are sufficient. Our proof technique proceeds by considering uniformly random ensembles over such states, and showing that the trace distance between these ensembles becomes arbitrarily small for sufficiently large \(n\) unless the number of copies is at least \(\Omega (n / \log n)\). We discuss implications for testing graph states and computing the generalised geometric measure of entanglement.

Numerically Benchmarking Optimisers for Quantum Algorithms

I have worked on several projects connected to this topic over the years. Most recently, I interned at Phasecraft (a quantum computing startup, focused on near-term applications and software) in the summer of 2022, and remained as a consultant with the company until December 2024. I essentially worked on the question: which are the best optimisers to use in variational quantum algorithms? This work involved a great deal of coding in Python, and running large scale numerical experiments on high-performance clusters.

I also interned with Entropica Labs (a Singapore based quantum computing startup) in 2019, working on optimisation techniques for the quantum approximate optimisation algorithm.

Prior to this, I worked in the Computer Science department at the University of Sheffield, looking at optimisation techniques in quantum simulation (Trotter-Suzuki formulas).

Paper: Benchmarking a wide range of optimisers for solving the Fermi-Hubbard model using the variational quantum eigensolver, arXiv, 2024.

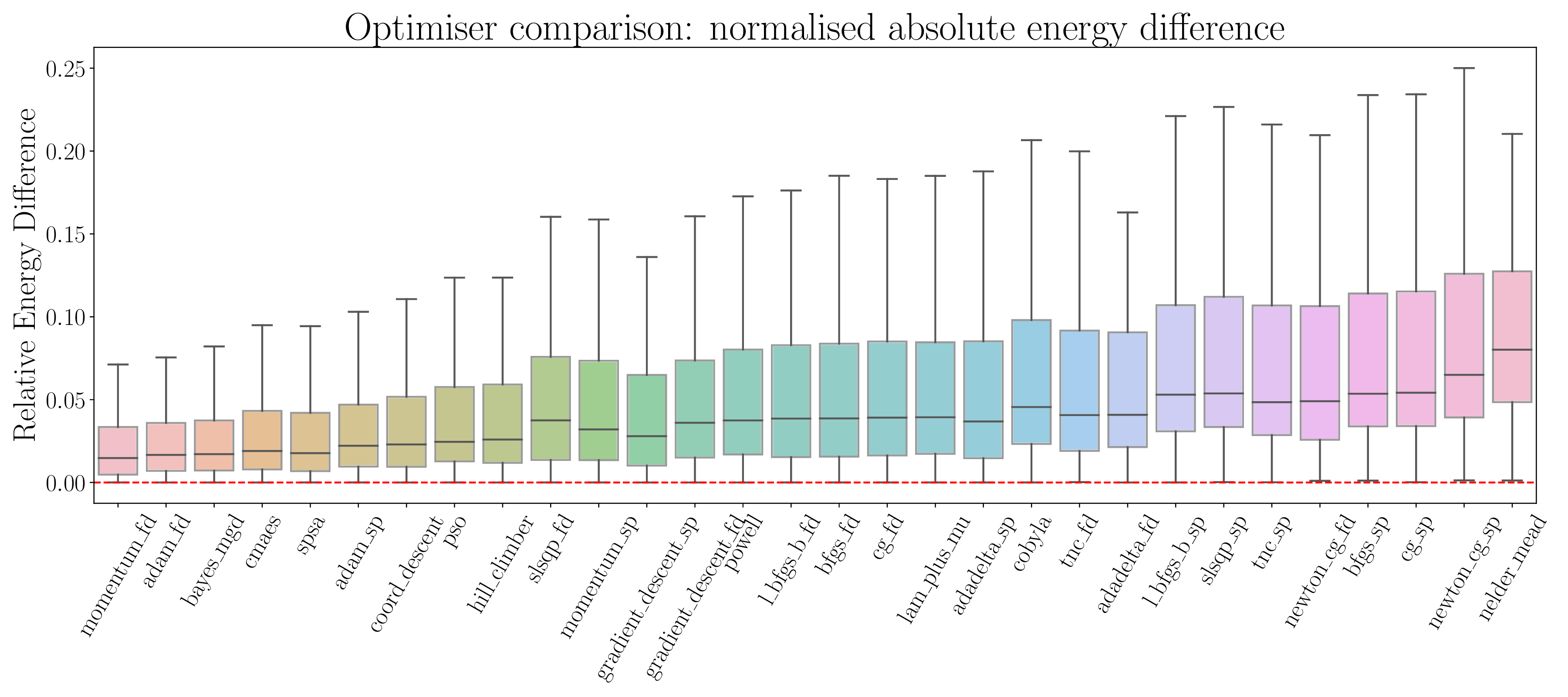
Abstract

We numerically benchmark 30 optimisers on 372 instances of the variational quantum eigensolver for solving the Fermi-Hubbard system with the Hamiltonian variational ansatz. We rank the optimisers with respect to metrics such as final energy achieved and function calls needed to get within a certain tolerance level, and find that the best-performing optimisers are variants of gradient descent such as Momentum and ADAM (using finite difference), SPSA, CMAES, and BayesMGD. We perform gradient analysis, and observe that the step size for finite difference has a very significant impact. We also consider using simultaneous perturbation (inspired by SPSA) as a gradient subroutine: here finite difference can lead to a more precise estimate of the ground state but uses more calls, whereas simultaneous perturbation can converge quicker but may be less precise in the later stages. Finally, we study the quantum natural gradient algorithm: we implement this method for 1-dimensional Fermi-Hubbard systems, and find that whilst it can reach a lower energy with fewer iterations, this improvement is typically lost when taking total function calls into account. Our method involves performing careful hyperparameter sweeping on 4 instances. We present a variety of analysis and figures, detailed optimiser notes, and discuss future directions.

Paper: Optimising Trotter-Suzuki Decompositions for Quantum Simulation Using Evolutionary Strategies, GECCO, 2019.

Abstract

One of the most promising applications of near-term quantum computing is the simulation of quantum systems, a classically intractable task. Quantum simulation requires computationally ex- pensive matrix exponentiation; Trotter-Suzuki decomposition of this exponentiation enables efficient simulation to a desired accuracy on a quantum computer. We apply the Covariance Matrix Adap- tation Evolutionary Strategy (CMA-ES) algorithm to optimise the Trotter-Suzuki decompositions of a canonical quantum system, the Heisenberg Chain; we reduce simulation error by around 60%. We introduce this problem to the computational search community, show that an evolutionary op- timisation approach is robust across runs and problem instances, and find that optimisation results generalise to the simulation of larger systems.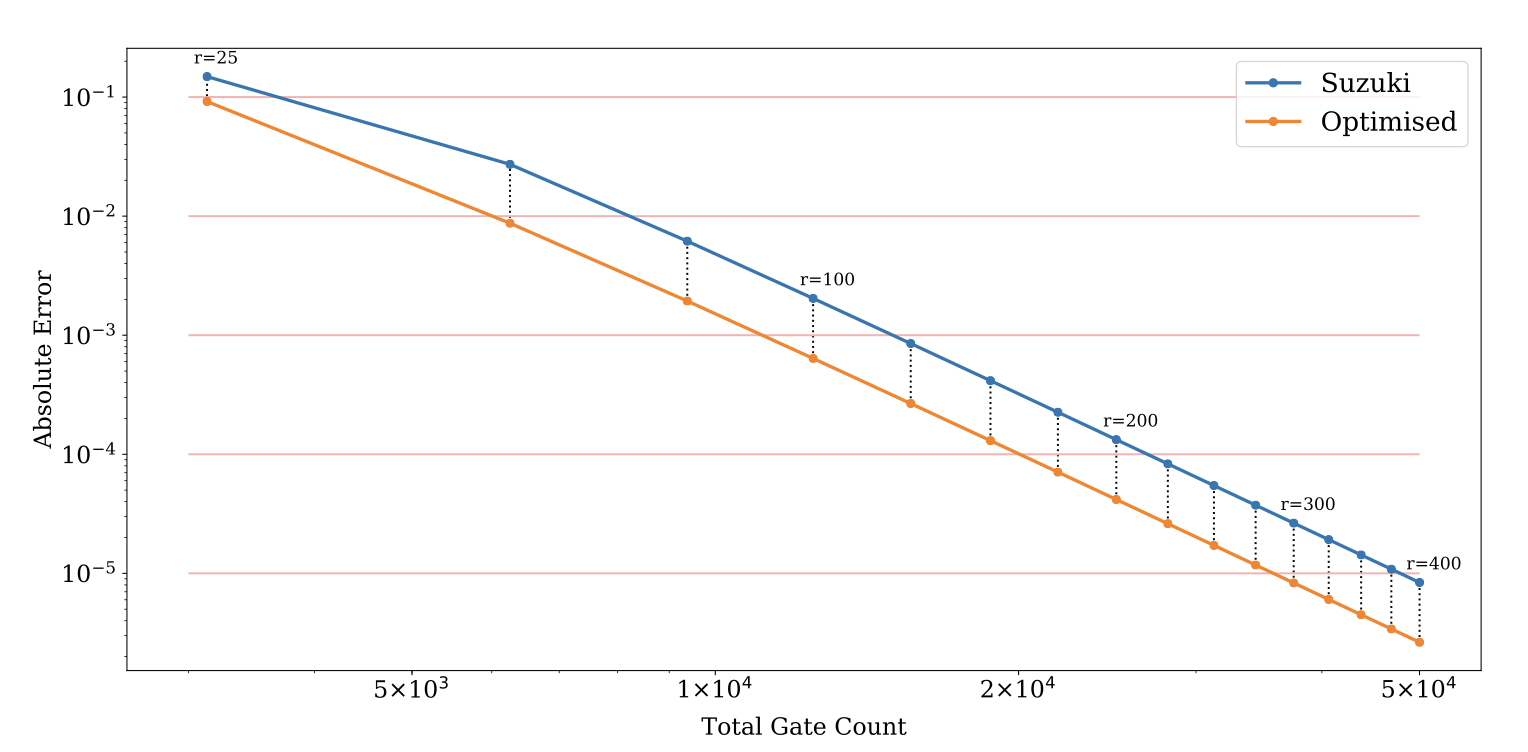

High-dimensional Quantum Systems

Paper: Simulability of high-dimensional quantum measurements, PRL, 2022.

Abstract

We investigate the compression of quantum information with respect to a given set \(\mathcal{M}\) of high-dimensional measurements. This leads to a notion of simulability, where we demand that the statistics obtained from \(\mathcal{M}\) and an arbitrary quantum state \(\rho\) are recovered exactly by first compressing \(\rho \) into a lower dimensional space, followed by some quantum measurements. A full quantum compression is possible, i.e., leaving only classical information, if and only if the set \(\mathcal{M} \) is jointly measurable. Our notion of simulability can thus be seen as a quantification of measurement incompatibility in terms of dimension. After defining these concepts, we provide an illustrative examples involving mutually unbiased basis, and develop a method based on semi-definite programming for constructing simulation models. In turn we analytically construct optimal simulation models for all projective measurements subjected to white noise or losses. Finally, we discuss how our approach connects with other concepts introduced in the context of quantum channels and quantum correlations.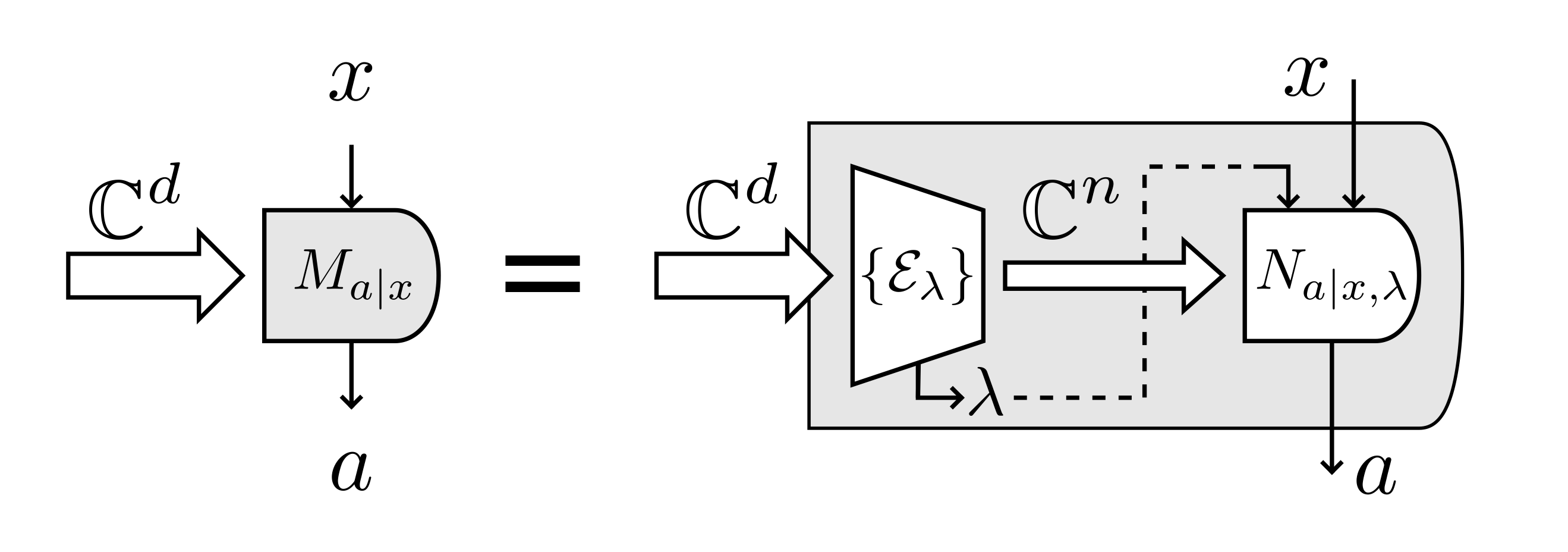

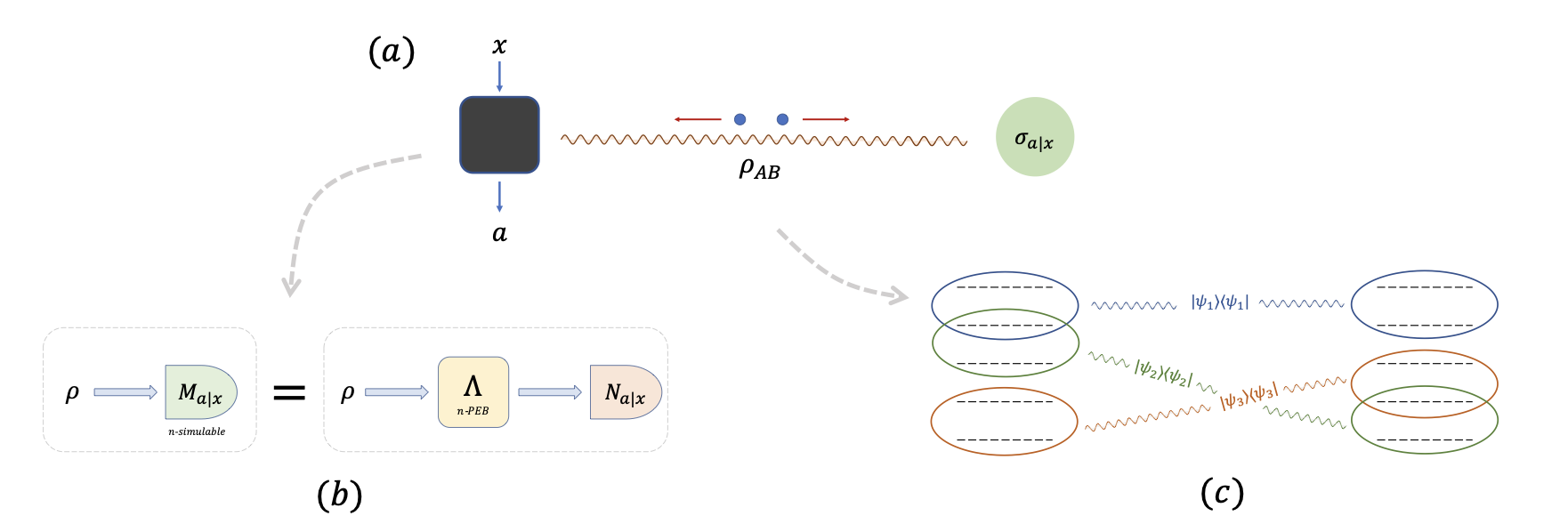
Paper: Equivalence between simulability of high-dimensional measurements and high-dimensional steering, PRA, 2023.

Abstract

The effect of quantum steering arises from the judicious combination of an entangled state with a set of incompatible measurements. Recently, it was shown that this form of quantum correlations can be quantified in terms of a dimension, leading to the notion of genuine high-dimensional steering. While this naturally connects to the dimensionality of entanglement (Schmidt number), we show that this effect also directly connects to a notion of dimension for measurement incompatibility. More generally, we present a general connection between the concepts of steering and measurement incompatibility, when quantified in terms of dimension. From this connection, we propose a novel twist on the problem of simulating quantum correlations. Specifically, we show how the correlations of certain high-dimensional entangled states can be exactly recovered using only shared random- ness and lower-dimensional entanglement. Finally, we derive criteria for testing the dimension of measurement incompatibility, and discuss the extension of these ideas to quantum channels.

Paper: Certifying high-dimensional quantum channels, arXiv, 2024.

Abstract

The use of high-dimensional systems for quantum communication opens interesting perspectives, such as increased information capacity and noise resilience. In this context, it is crucial to certify that a given quantum channel can reliably transmit high-dimensional quantum information. Here we develop efficient methods for the characterization of high-dimensional quantum channels. We first present a notion of dimensionality of quantum channels, and develop efficient certification methods for this quantity. We consider a simple prepare-and-measure setup, and provide witnesses for both a fully and a partially trusted scenario. In turn we apply these methods to a photonic experiment and certify dimensionalities up to 59 for a commercial graded-index multi-mode optical fiber. Moreover, we present extensive numerical simulations of the experiment, providing an accurate noise model for the fiber and exploring the potential of more sophisticated witnesses. Our work demonstrates the efficient characterization of high-dimensional quantum channels, a key ingredient for future quantum communication technologies.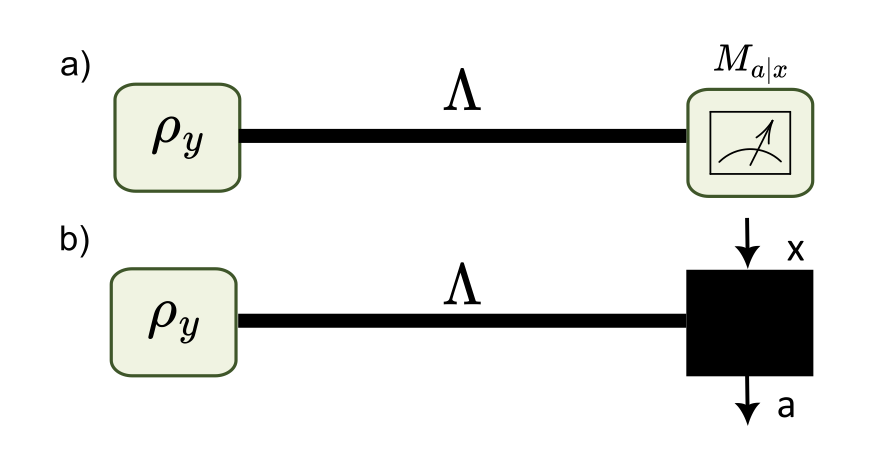

Quantum Steering in Networks

Paper: Network Quantum Steering, PRL, 2021.

Abstract

The development of large-scale quantum networks promises to bring a multitude of technological applications as well as shed light on foundational topics, such as quantum nonlocality. It is particularly interesting to consider scenarios where sources within the network are statistically independent, which leads to so-called network nonlocality, even when parties perform fixed measurements. Here we promote certain parties to be trusted and introduce the notion of network steering and network local hidden state (NLHS) models within this paradigm of independent sources. In one direction, we show how results from Bell nonlocality and quantum steering can be used to demonstrate network steering. We further show that it is a genuinely novel effect, by exhibiting unsteerable states that nevertheless demonstrate network steering, based upon entanglement swapping, yielding a form of activation. On the other hand, we provide no-go results for network steering in a large class of scenarios, by explicitly constructing NLHS models.